Rubik's cube - Edge Rotations - Details

Method 1 for rotating 2 edges

Initial formula	rotated by 1	rotated by 4	Variant
-T R T F R2 -F 2R -R F -R2 -F -T -R T -2R R	R T F R2 -F 2R -R F -R2 -F -T -R T -2R R -T	R2 -F 2R -R F -R2 -F -T -R T -2R R -T R T F	-T R T F R2 -F 2R2 -R2 F -R2 -F -T -R T -2R2 R2

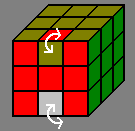
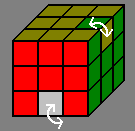
In this method, we first rotate one edge in 6 moves (in orange) while making sure that nothing else in the middle slice (between right and left faces) has changed. then we replace that edge by a different edge (white moves), and undo the first set of 6 moves (in cyan), and we restore the middle slice (white moves).
The 2nd and 3rd formulas show that by "rotating" a formula, we can end-up affecting different cublets.

Method 2 for rotating 2 edges

Initial formula	rotated by x	rotated by y	rotated by z
-F -R F -2R R -F R F D R2 -D 2R -R D R2 -D

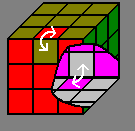
This method is based on the exchange of 3 edges (in white) followed by another exchange (in orange) of the same 3 pieces. Because the 2nd exchange swaps the pieces back into the same place with a different formula, it results in rotating 2 pieces. Also, those 2 formulas normally have 10 moves each, but they were chosen so that the last 2 moves of the 1st formula and the first 2 moves of the second cancel each other, to result in a 16 move formula.

Method 3 for rotating 2 edges

Initial formula	variant 1	variant 2	variant 3
-T -2B B T2 -2B2 B2 -T -F T -2B2 B2 T2 2B -B T F	-T -2B B T2 -2B2 B2 -T F2 T -2B2 B2 T2 2B -B T F2

In this method, we first rotate one edge in 6 moves (in orange) while making sure that nothing else in the front face has changed. then we replace that edge by a different edge (white move), and undo the first set of 6 moves (in cyan), and we restore the front face back in place (white move).

rotating 4 edges

Same face	Same slice
R -B -R B -T B T -2B 2R -R B -T -B T -B R B -2R 2B -B	-T -F R2 F T -R D F R2 -F -D 2R2 R2 D F R2 -F -D R -T -F R2 F T -2R2 R2
3 sides 20 moves	4 sides 26 moves

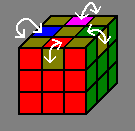
The first formula is based on an 8 move formula that rotates 2 edges on one side. Then the 2 edges are replaced by 2 other edges, and the 8 moves formula is made backward. Once simplified, it turns into a 20 move formula.
The second formula is based on the same principle than the first formula to rotate 2 edges. Once rotated, they are exchanged with 2 other edges on the same slice, then the initial formula is made backward.

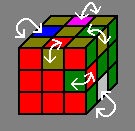
Rotating 6 edges

First formula	Second formula
R 2T R 2T R 2T R 2T R T R 2T R 2T R 2T R 2T R T R 2T R 2T R 2T R 2T R T	-F -T F T -F -T F T -F -T F -2F T 2F -T -2F T 2F -T -2F T 2F
2 sides 30 moves	2 sides 22 moves

The first formula is probably better for rotating all edges, but they are both too long. I'm working on finding more efficient formulas.

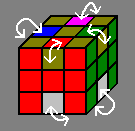
Rotating 8 edges

First formula	Second formula
2R -R 2B -B T2 2R -R 2B -B T2 F2 R2 F2 R2 F2 2R R 2B -B	2R R -2B -B 2R R -2B -B 2R R -2B -B
4 sides 19 moves	2 sides 12 moves

I first discovered the 19 move forumula, and later, trying to find a formula for 4 edges, I found the 12 move formula for 8 edges.
Note: the formula that rotates 8 edges in 19 moves also rotates Front and Bottom centers 180°.


Click here if you need to understand the notation used on this page