Rubik's cube - Edge swapping - Details

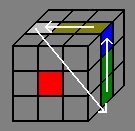
Method 1 for exchanging 3 edges

Initial formula	rotated by 1	rotated by 4	Variant

In this method, we ...

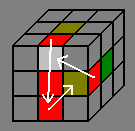
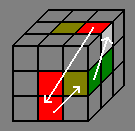
Method 2 for exchanging 3 edges

Initial formula	rotated by 1	rotated by y	rotated by z
-T R T 2R -R -T -R T R -2R	R T 2R -R -T -R T R -2R -T

This method is based on ...

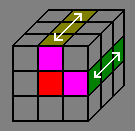
Methods for exchanging 2x2 edges

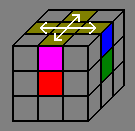
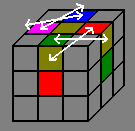
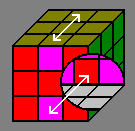
Adjacent sides	Opposite sides	Same side		Crossed	Swap&Rotate
R2 T2 R2 T2 R2 T2	T2 2R2 R2 T2 2R2 R2	2R2 R2 -T F2 2R2 R2 F2 2R2 R2 T 2R2 R2	T -R -T R -T R T R -T -R T R T R2 -T -R T	2R2 R2 T 2R2 R2 T2 2R2 R2 T 2R2 R2	R -F 2T2 T2 F -R T2 R -F 2T2 T2 F -R T2

In the first column a few 180 turns will eventually exchange 2x2 edges as shown. Same with the second column.
In the third column, we move 2 opposite edges from the top face to the bottom face, right under the other 2, use the 2nd column formula, and restore the edges at their original place.
In the fourth column, you will find what Xavier Morin calls his PLL Z formula. The advantage is that it is only using 2 faces to execute it, the drawbacks are that it also rotates 2 centers and takes 17 moves.
in the 5th column you will find a relatively simple way to exchange 2 times, 2 opposite edges on the same side.


Click here if you need to understand the notation used on this page