
Everyone understands and encourages long hours of practice for sports, dance, music, and many other endeavors. Logic should be no different.
No one doubts that Olympic athletes and professional sports stars practice their craft constantly in spite of their obvious talents. Indeed, many motivational books and lectures often focus on the life story of someone who has "made it" in sports through hard work and determination in spite of abilities that do not make them stand out among their peers. Ask someone to practice thinking ... Or worse, practice logic ... Suddenly all of those lessons do not seem to apply, even though most of life's challenges come from making important decisions off the sport's field and require most of all, the ability to think clearly.
Many people, especially those that enjoy working puzzles of any type, believe that practice does make one a stronger and more agile thinker (to use the sports metaphor) and that such abilities do carry over to the rest of life. Many start every morning with a puzzle as a type of mental calisthenics to get "warmed up. " Moreover, education research has shown that active mental exercises, even simple ones like reading a book, have a more positive impact on learning than passive activities, such as watching TV. Puzzles of any sort, therefore, offer an even greater opportunity to exercise your mind because they require a more active involvement in the material than reading. Just as word puzzles can exercise verbal skills and math puzzles can exercise math skills, logic puzzles exercise logic and deductive reasoning skills that can help lead to clear-minded decision making.
Unfortunately, even some ardent puzzle lovers have found Sudoku-type logic puzzles too hard or difficult, and in the final analysis, simply not fun. Starting a brief survey of why these people did not work Sudoku puzzles quickly revealed the obvious: most puzzles are published for those people who already know and love group logic puzzles. Even puzzles marked as "Easy" in newspapers and magazines can prove daunting to someone who has never worked a Sudoku puzzle unless they have someone available to tutor them briefly about the basics. At the very least, they need step-by-step solutions to puzzles describing how someone can deductively reason from the particular puzzle that they are currently working on to the completed grid. The completed grids published with most Sudoku puzzles as puzzle solutions, in contrast, only tell you whether you have arrived, not how to get there. Although we do not expect students to learn a subject like math from just a set of problems and solutions, with no explanation or tutoring, most sources of logic puzzle do exactly this. These publications limit their audience to those who already know and like such puzzles and, more importantly, limit their usefulness in teaching logic in an educational environment.
For many people who enjoy working logic puzzle, it is simply "obvious" that puzzles are a good tool for teaching logic and nothing further needs to be said. For people who enjoy these puzzles and understand how to work them, that is true. For many others, however, especially for children and those who teach them, there are a number of challenges and potential pitfalls facing the use of puzzles to teach logic in the general population and in schools.
Teaching logic is difficult. Teaching guessing is unnecessary. In order to teach logic using group logic puzzles like Sudoku, there must be at least one purely deductive logical path from every puzzle to its solution that requires no guessing or backtracking. Students must know the easiest way to solve the puzzle is logic so that they actively and habitually look for it. Purely deductive solutions for most published Sudoku puzzles often exist, but deductive solutions are rarely guaranteed. This is one barrier to the effective use of existing puzzle sources to teach logic. Another barrier to the use of puzzles is the lack of availability of step-by-step deductive solutions. Detailed step-by-step instructions are required not only for instructors who wish to use puzzles, but may not have the time to work each puzzle before the students, but also for anyone who has never worked such a puzzle and wishes to teach themselves. Existing publishers for Sudoku puzzles do not provide step-by-step instructions that describe what values can be placed where in a puzzle, and why. Indeed, a number of puzzles in some publications have been found to have no deductive solution and require guessing and backtracking. These are usually "symmetric" puzzles, so named because they are constructed from a solution grid using a pattern of empty cells that is reflectively symmetric about one or more axis. Symmetric puzzles are an attempt to approximate puzzle difficulty by use of these patterns. When puzzles are rated quantitatively, however, symmetric puzzles have been found to provide only a coarse probabilistic approximation to puzzle difficulty in terms of the number of deductive steps required to solve the puzzle.
Like any other educational tool, the effectiveness of using puzzles to teach logic requires educational materials, including puzzles, strategy guides, step-by-step solutions, and hints, that are always correct. Incorrect puzzles teach students that logic and deduction do not work. Incorrect puzzles teach students to guess rather than to reason and solve. Incorrect puzzles drive students away from logic. Students must know that the effort expended in logically deducing solutions is not a wasted effort or the puzzles are no longer fun and become just another school chore. Puzzle correctness can be guaranteed by the use of a set of automated tools and stringent quality control measures that eliminate errors in the puzzle generation, rating, and type setting processes.
The educational effectiveness of puzzles is also strongly dependent on matching puzzle difficulty to the solver's current abilities. Puzzles that are too hard make students frustrated and risk the most important advantage they have for teaching: making learning fun. Puzzles that are too simple have little teaching value or make students bored, also risking the fun factor. Thus, educational logic puzzles require a very accurate puzzle difficulty rating system. This, however, is yet another barrier to the effective use of existing puzzle sources. Most publishers separate puzzles into sections with labels, such as Easy, Medium, and Hard. The detailed quantitative classification algorithm described here , however, has been used to show that there is tremendous overlap in the difficulty ratings in sections of some existing publications with supposedly different difficulty classifications. Indeed, in one publication there were puzzles that required guessing (i.e. they were nondeterministic) in the section labeled "medium" rather than in the section labeled "hard," although there were fewer nondeterministic puzzles in that section. In addition, the puzzle with the most difficult deterministic solution in the entire book was found in the medium section, not the hard section.
Carefully calibrated puzzle difficultly is only as effective as the availability of puzzles at a wide variety of difficulty levels. Working puzzles provides vital practice of logic skills, but these skills must be exercised regularly and the exercise itself must be well-suited to each person's current ability level so that they are challenged without being overwhelmed. This requires puzzles at many difficulty levels, from very simple to extremely challenging, for puzzles of every type. The easy availability of puzzles at the appropriate level of difficulty helps students make steady progress without risking frustration or boredom.
There are several reasons why many different types of logic puzzles are essential to teaching logic. First, new and different puzzle types help to keep and hold the interest of students. If they are not fun, then one of the key advantage of puzzles is lost. Second, smaller puzzles are inherently easier to work than larger puzzles and choosing the type of puzzle is the first and most important part of selecting the appropriate difficulty of a puzzle for a particular audience. A simple 3x3 grid puzzle, such as the one shown here,

may prove challenging for most preschool children, but boring and unappealing to older grades. Larger group sizes (such as 12 or 16) also greatly increase the difficulty of a puzzle, more so than just the overall size. For example, a 12x12 grid with 12 distinct group values and an overall size of 144 cells can be much more difficult than one of the Sunday newspaper puzzles with five overlapping standard Sudoku puzzle with 9 distinct group values on a 21x21 grid with an overall size of 369 cells. Third, and perhaps most importantly, new types of puzzles help students generalize their solving techniques and logic skills rather than focusing on the puzzles themselves and developing mental habits that are useful only in solving one particular type of puzzle, such as the traditional Sudoku puzzle. Since group logic puzzle are mathematical constraint satisfaction problems, there is no simple algorithm to deductively solve all such puzzles, so children can (and should) be encouraged to discover their own puzzle solving rules and heuristics and then check them for correctness and usefulness. Since the rules for checking these puzzle are simple enough that even young children can understand the rules of the smaller puzzles, group puzzles offer a wonderful opportunity to combine both logic and fun for everyone.
Another way to focus on learning logic is to solve one of the harder or larger puzzles using a grid that shows the step in which each empty cell can be deduced using the rules outlined in the general strategy guide. Knowing which cells can be filled in given the current state of the puzzle is often the hardest part of finding a solution. Specifying that information in the puzzle itself eliminates the question of where to work on the puzzle next and allows the solver to focus on looking for a specific solution using only logic, since they know there has to be a way for the value of the cells in the current step to be deduced from the given information. While this approach can be used for any puzzle type and any difficulty level, it is particularly useful for very large or very difficult puzzles where there are many more options to consider that lead to a solution. For example, in the tournament-level puzzle shown here, are 25 dependent steps that lead to the solution using the standard algorithm.

The step number is annotated in the top right corner of each empty cell. All cells with the same number can be logically deduced independently of one another from only the initial givens and all the cells with lower step numbers. Using these types of puzzles annotated with the solution step information can change the problem solving experience significantly because the frustration associated with fruitlessly searching for the next move can be avoided for those that have not yet acquired those skills. Thus, these types of puzzles with step numbers annotated in all the empty cells are, in a very real sense, a new type of puzzle in and of themselves.
Another variation on this type of puzzle is to fill in some, but not all, of the step numbers on the harder or larger puzzles. For example, annotating the first several steps of puzzles provides the opportunity for solvers to tackle harder puzzles than they usually attempt by making it easier to solve the puzzle to a level of difficulty that they are more accustom to coping with.
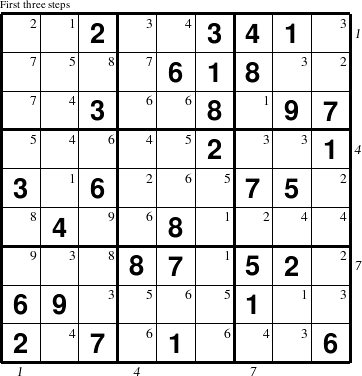
Annotating the last few steps is another possible variation that outlines to the solver the more difficult areas of the puzzle to help them avoid wasting effort, without providing them with an explicit road map of how to go about solving the puzzle.
The beauty of these types of puzzles is that there are an enormous number of logical ways to solve each puzzle and many different heuristics and strategies for each solver to discover, practice, and evaluate. The key is to enable this type of learning without limiting future opportunities for additional learning, by providing a wide variety of puzzles and only general guidance.
The short answer is that group puzzles are a generalization of Sudoku puzzles, just as Sudoku puzzles are a generalization of Latin Squares. The long answer requires a brief history of Sudoku puzzles.
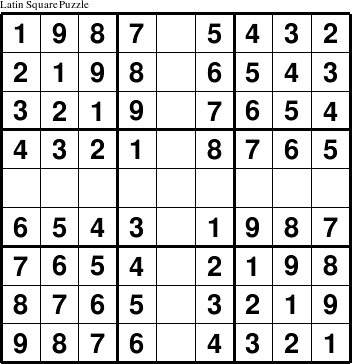
Sudoku puzzles are often described as a special type of Latin Squareof size 9 that has additional constraints. A Latin Square is a well-known mathematical construct that has been the subject of study for decades. A Latin Square of size N is defined to be a square matrix with N rows and N columns containing only integers from 1 to N arranged so that there are no duplicate integers in any row or column. A Latin Square the size and shape of a traditional Sudoku puzzle is, therefore, a Latin Square of size 9.

The particular Latin square shown here, however, is not a valid Sudoku puzzle solution because (among other problems) the 3x3 square in the upper left corner has duplicate integers and is missing some of the integers, such as 4, 5, 6, and 7. It does however meet all the constraints of a Latin Square because each row and column contains a full set of the integers ranging from 1 to 9.
A Latin Square puzzle can be generated from a Latin Square by replacing some of the numbers with empty cells.
Care must be taken when selecting which cells to leave empty or the puzzle that is generated from the Latin Square may not be solvable. In order to create a useful puzzle, the values of all of the the empty cells must be able to be determined by examining the numbers remaining in the puzzle, given the row and column group constraints which define a Latin Square. If too many cells are left empty, there may be more than one valid Latin Square that contain the initial values given in the puzzle. Even greater care must be taken to ensure that the puzzle has a purely deductive deterministic solution that does not require guessing or backtracking.
Although not all Latin squares are valid Sudoku puzzles, the reverse is true: all traditional Sudoku puzzles are valid Latin Squares. This is because a traditional Sudoku puzzle constrains not only the rows and the columns to be complete groups of the integers from 1 through 9, but also constrains all of the 3x3 squares to be complete groups as well. There are many variations on Sudoku puzzles that typically fall into several different categories: group sizes other than 9, additional constraint groups, such as diagonals, inner squares or jigsaw shapes, groups of unique values other than numbers (such as letters) and multiple overlapping puzzles of various types. One thing all of these puzzles types have in common is the specification of a group of unique symbols or values that make up each constraint group defined for a particular type of puzzle. Like Latin Squares, elements of a complete valid Sudoku square can be removed to create a puzzle where the missing items can be logically deduced from the remaining values and the constraints on the groups.
Group puzzles are a generalization of Sudoku puzzles in that groups need not be contiguous shapes, rows and columns need not be groups (i.e., the puzzle need not be a valid Latin Square), and the values in the groups can contain duplicates.
A non-contiguous group is a group where the members of the group are not immediately next to each other in the puzzle, such as the outside corners of a 4x4 puzzle.
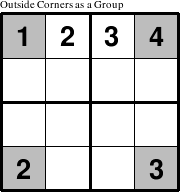
In this puzzle, the non-contiguous outside corners of the puzzle form a group in addition to the contiguous 4-element rows, columns, and 2x2 squares. Non-contiguous groups are logically no different from puzzles with only contiguous groups, but they pose two different challenges for human puzzle solvers. The first difficulty concerns how to visually identify which cells in a non-contiguous group actually make up a non-contiguous group. The most common way to show this is to use a single color or shade of grey to indicate that the cells of the same shade belong to the same group. In cases where the non-contiguous group follows a clear enough pattern, such as the upper right corners of every rectangle, the group members may be outlined rather than shaded. The second difficulty is developing the habit of perceiving diverse disconnected cells as part of the same group.
Group puzzles that are not valid Latin Squares also pose a additional challenges for human puzzle solvers for several reasons. First, rows and columns are visually obvious groups for human solvers that are difficult to ignore. Second, in-grained habits are often difficult to break. Moreover, additional constraint groups can make logical deductions easier when there are more unknowns, so removing the constraints on rows or columns can make it more difficult to deduce other unknowns in the puzzle. For this reason, non-latin puzzles typically require additional constraint groups that take up the slack for a missing row or column constraint. The next example illustrates one of these types of group puzzle that is neither a traditional Sudoku puzzle nor a Latin Square.

In this puzzle, rows are not constrained to be groups, but the columns, 2x3 rectangles, the one diagonal, and the group comprised of the upper right corners of the 2x3 rectangles are all constraint groups.
Group puzzles, unlike traditional Sudoku puzzles, can contain repeated elements in a group. An example of one such puzzle uses the familiar Sudoku 9x9 grid with a group size of 9, but the group contains only the numbers 1 through 8 with the value 1 present twice in each row, column, and 3x3 square.

In other words, the group for the puzzle is (1, 1, 2, 3, 4, 5, 6, 7, 8). These types of puzzles offer a different type of challenge, since groups with duplicate values can make for more difficult puzzles that requires new strategies to deal the the fact that some symbols can be repeated.
Adding new and different puzzle types is one of the important ways, from a teaching perspective, to keep puzzle solving fresh and useful Although creators of Sudoku puzzles have historically limited themselves to a relatively small number of puzzle types with a somewhat ad-hoc collection of names, the goal of introducing dozens or even hundreds of new group puzzle types into common usage indicates that it would be useful to define a naming convention for puzzles, such as the one described below, that expresses similar attributes.
One of the most important attributes of a group puzzle is the size of its constraint group. For traditional Sudoku puzzles which require the placement of the values 1 through 9 exactly once in each of the 9 rows, columns, and 3x3 squares, the group size is 9. The puzzles that consist of 5 overlapping traditional Sudoku puzzles, also have a group size of 9 (even though the 5 overlapping puzzles are part of a larger 21x21 grid) because there are exactly 9 different values that must be placed in each row, column, and 3x3 square. The standard name for a traditional Sudoku puzzle in this new naming convention, therefore, would be Sudoku-9.
Group puzzles of size 9 that do not require both the rows and columns to be constraint groups are not valid latin squares. The standard name would reflect this lack of constraints with the name Nonlatin-9. Similarly, the Sudoku part of name Sudoku-9 implies that all of the rows and columns are constraint groups. Thus, in the standard naming convention, any puzzle named Sudoku-N has a group size of N with all of the rows and columns being constraint groups.
Group sizes that are integer squares, such as 4, 9, 16, and up, have the obvious square constraint groups of 2x2, 3x3, and 4x4, respectively. Puzzle sizes that are not integer squares, but are even integers, can be divided into N rectangles of the same shape and orientation. These rectangles can be oriented either horizontally or vertically. The horizontal layout is considered standard and requires no addition to the standard name. The vertical layout is designated in the name by adding the word up after the size. Thus, the name Sudoku-6 indicates a puzzle that has six 3x2 horizontal rectangle constraint groups and a Sudoku-6up puzzle has six 2x3 vertical rectangles.
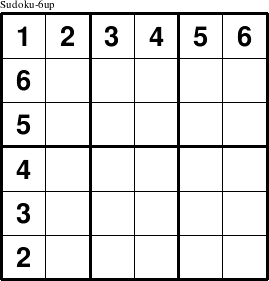
A more common name for a Sudoku-6 puzzle is Sudoku-Junior just as the common name for a Sudoku-9 puzzle is just Sudoku.

Some group sizes, such as 12, can be divided into either 2x6 or 3x4 rectangles. Puzzles with narrow rectangles are usually more difficult to create and solve, so the more square-like shapes are favored in the standard naming. The name Sudoku-12up, therefore, refers to a puzzle with 12 vertical 3x4 rectangles.
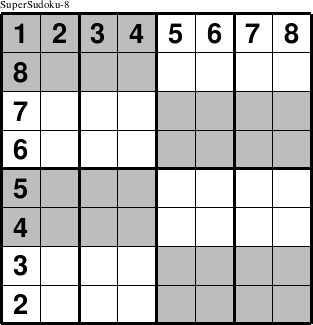
There is no logical limitation on creating group puzzles with both horizontal and vertical rectangles as constraint groups. The primary limitation is how to display the puzzles in such a way so as to show both the horizontal and vertical rectangles as constraint groups. The compromise described here appears to be the best solution: display the puzzle with the vertical rectangles outlined and the horizontal rectangles alternately shaded. If all of the horizontal rectangles were shaded, the entire puzzle would be shaded. By shading them in a checker board fashion, the horizontal rectangles are fairly clearly marked. The standard naming convention for puzzles in which both the horizontal and vertical rectangles are constraint groups is to attach the prefix "Super." to the standard name. Thus, a group puzzle of size 8 with both the 2x4 and 4x2 rectangles as constraint groups would be called SuperSudoku-8.
Group sizes that are neither integer squares nor even integers cannot be divided into N identical rectangles, so some other shapes must be devised. The simplest solution is to use irregular contiguous jigsaw-puzzle shapes. There are many ways to divided squares into jigsaw shaped pieces of size N. One possible set of jigsaw puzzle shapes is illustrated for the Sudoku-5 puzzle shown here.

Not all possible divisions into jigsaw-puzzle type shapes, however, result in puzzle types that have any solutions. In general, the shapes cannot overlap any particular row or column in too many cells, or the resulting puzzle definition has few or no solutions that can be turned into puzzles. Because there are so many possible jigsaw puzzle shapes, multiple types of jigsaw puzzles may be defined for a particular group size. The naming convention for these additional puzzles of the same size is to add an additional letter following the standard name. For example, the following Sudoku-5B puzzle has a different set of jigsaw puzzle shapes from the previous Sudoku-5 puzzle as shown here.

The letter 'B' is used in this name because it is assumed that the initial jigsaw puzzle of the particular size is the 'A' puzzle. The third variant of size 5 would be named Sudoku-5C, etc.
One fairly common addition to the the standard row, column, and rectangular constraint groups is to add the diagonals of the square of size N as constraints. The two diagonals represent constraints in addition to the other constraints, even though there are only two diagonals and not every cell is a member of a diagonal constraint. The standard naming convention is to add the suffix "-X" to a based puzzle type. For example, a Sudoku-9-X or Sudoku-X puzzle is a standard Sudoku puzzle of size 9 with the addition of both diagonals as constraint groups.
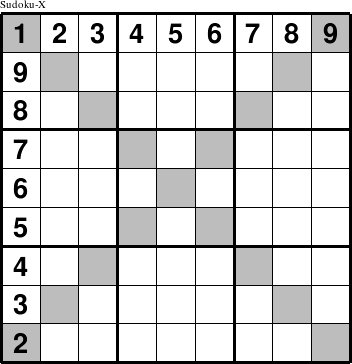
In order to visually show the presence of the diagonals as a constraint group, they are usually shaded, as shown here. The naming convention of adding an 'X' to the puzzle name is because the two shaded diagonals look like the letter X. Adding both diagonals to most puzzles smaller than size 8 results in a puzzle definition that has no solutions or puzzles. For some of these, a single diagonal can be added to produce puzzles. The standard naming convention for puzzles with a single diagonal rather than both diagonals is to append a 'D' to the name rather than an 'X'.
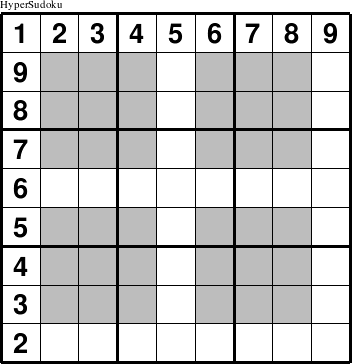
Another way to define puzzles with additional group constraints is to have interior shapes that overlay several of the standard rectangles or squares of an existing puzzle. These puzzles are named by adding a prefix of "Hyper" to the standard puzzle name, following the pattern set by the most common puzzle of this type, the HyperSudoku puzzle. The HyperSudoku puzzle, shown here, derives its name from the fact that it adds a fourth constraint group to the usual three constraint groups of a traditional Sudoku puzzle, just as a hypercube adds a fourth dimension to the normal three dimensional of a traditional cube.
There are many different types of interior shapes that can be chosen for a Hyper Sudoku puzzle. As usual, the most difficult part is to design the puzzle in a way that clearly indicates which cells are in a group. Most often this is done using shading. For example, the HyperSudoku-12 puzzle has four 4x3 interior rectangles and one 6x2 rectangle, all shaded gray to show their location.
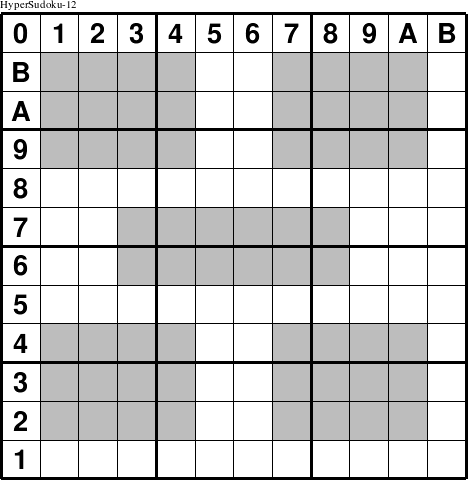
Like diagonals, adding too many interior rectangular constraints or not overlapping the interior shapes over enough other puzzle constraint groups can severely limit or eliminate puzzle solutions.
Overlapping interior shapes can be logically defined and implemented, but the problem is finding ways to express the constraint groups clearly to the solver. One way to show an additional overlapping set of interior shapes, is to use an additional shade of gray, another color, or a shading pattern for the second set of constraint groups. All such indicators, however, must be clearly distinguishable by the solver even when the groups overlap. The HyperSudoku-X puzzle is one such puzzle with two different overlapping shaded constraint groups. A HyperSudoku-X puzzle combines the constraint groups of a HyperSudoku and a Sudoku-X puzzle, as the name implies.

A non-contiguous constraint group has group elements that are not immediately next to each other in the puzzle, such as the outside corners of a Sudoku-4 puzzle.

In this puzzle, the non-contiguous outside corners of the puzzle form a constraint group in addition to the contiguous 4-element rows, columns, and 2x2 squares. No standard naming convention for non-contiguous groups has been defined, as yet, and ad-hoc abbreviations for the non-contiguous groups is recommended. Thus, the Sudoku-4 puzzle in which the outside corners also make up a constraint group, the name is chosen to be Sudoku-4-OC. The most common way to show this is to use a single color or shade of grey to indicate that the cells of the same shade belong to the same group. In cases where the non-contiguous group follows a clear enough pattern, such as the upper right corners of every rectangle, the group members may be outlined rather than shaded. For example, the following puzzle is named Sudoku-6up-UR-D because the base puzzle is a Sudoku-6up with the additional constraints that the upper-right corners of the rectangles are a constraint group, as is the single descending diagonal.

A signature puzzle is a standard group puzzle type in which the usual sequence of numbers, or letters for the larger puzzles, are replaced with a specific set of letters or numbers that spell out a word or message.

One singularly appropriate signature puzzle for educational purposes, is one that is created using a traditional Sudoku puzzle and substituting the letters that make up the word "EDUCATION" for the digits 1 through 9. If a puzzle were created randomly using these letters, however, there is little chance of the word "education" appearing anywhere in the puzzle. So, for a signature puzzle to be recognized as such, the word should appear in order in one of the contraint groups. The first row of the puzzle is the most prominent location to place the word or phrase when creating a signature puzzle.
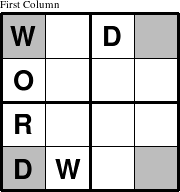
The signature, however, can be place in other prominent places, such as the first column, or any constraint group of any type of puzzle.

In fact, a signature can be place in more than one spot in a puzzle. Placing the signature in more than one spot in a puzzle, however, can be challenging for two reason. First, it is difficult in most puzzles to place a signature that is readable in two different constraint groups that does not violate the group constraints of the puzzle. For example, you may want to place the signature in both the first column and the first row. This is not possible using any of the group puzzles that have the traditional Sudoku contraint groups consisting of all rows and columns because it results in duplicate letters in the first rectangle. However, in some groups of certain types of puzzles, such as HyperSudoku puzzles, it can be done.
The instructions for a traditional Sudoku puzzles are simple: Place all of the elements 1 through 9 exactly once in each row, column, and 3x3 square. The beauty, as well as the challenge, of all types of group logic puzzles like Sudoku is the minimalist nature of these rules.
Knowing how to check for a correct solution, however, does not mean that the solution is easy to logically deduce. In fact, the class of computer science problems that have a simple solution check but no known optimal algorithm are proven to be the most difficult class of problems to solve, with the optimal solutions requiring guessing at every possible solution and checking whether it is valid. For these types of puzzles, there does not exist a single set of rules that can guarantee a set of solution steps that leads the solver deductively from puzzle to solution, for every possible puzzle that has a solution. Thus, computers and humans alike, must guess at solutions for certain Sudoku and group puzzles and check the group constraints to see whether the solution is in fact valid. Although computers can guess, check, and backtrack quickly if they are wrong, puzzles designed to be worked by humans should not require guessing or backtracking if the purpose is to teach deductive logic. For teaching purposes, puzzles should be selected only if there exists a sequence of deductive step-by-step moves that lead from the puzzle to the solution.
Although there does not exist a simple definitive set of rules for deductively solving all puzzles, there do exist general strategies, often called heuristics, that can be used to solve most puzzles. For group puzzles there are two basic strategies that encompass most of the strategies in common use: find the only spot in a particular group where a certain value can occur (given the group constraints) and find the only value that can be placed in a particular spot (given the group constraints).
The first and most common approach to solving these puzzles is to figure out all the spots in a constraint group where a particular value cannot be placed, and when there is only one spot left in the group where it is allowed, you have found the spot where the value must be put. To do this, check if one value in the puzzle appears in several places and constrains where that value can appear in another group. In example 1, the value 4 must appear at the
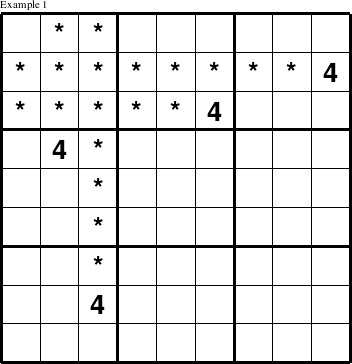
top of the first column at coordinates (1, 1) because the value 4 appears outside the 1st 3x3 square (top left 3x3 square) in rows 2 and 3 as well as columns 2 and 3. So, the only spot left for 4 in the 1st 3x3 square is at (1, 1).
Although the application of this technique to 3x3 squares is by far the most common way for people to work towards a puzzle solution, the same logic applies to rows and columns as well. In the next puzzle, the value 5 must appear at (1, 1) because the 5 in the second row means that 5 cannot appear in the last 3 columns of row 1, and the 5 in the fifth row means that it cannot appear in column 5 of row 1. Furthermore, the 5 in the last row rules out a 5 in column 3, and there are already values of 2, 3, and 4 in the second, fourth, and sixth columns of row 1.
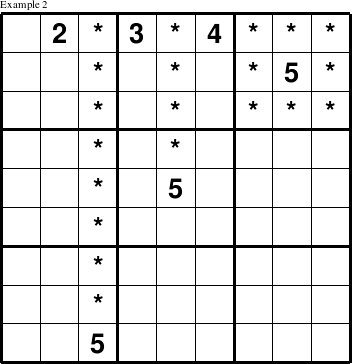
Thus, the only spot left for 5 in the 1st row is at (1,1).
The values in columns can be similarly deduced. In the puzzle below, a 6 must be placed at (1, 1) because the value 6 in the third column eliminates the last three rows as spots for a 6 in column 1, and the values 1, 2, and 3 in column 1 as well as the 6s in columns 5 and 9 rule out the remaining spots.
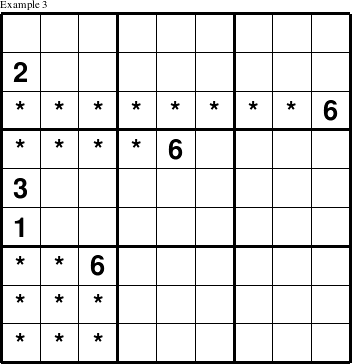
Thus, the only spot left for 6 in the 1st column is at (1,1).
This same strategy can be used to deduce values in other types of group puzzles as well. In the HyperSudoku puzzle below, the four inner squares that are colored gray are additional groups that must also contain the values 1 through 9.
Here, the only spot left for a 4 in the 1st 3x3 square is at (1, 2), because the 4 in the last row rules out all of the spots in the first column, and the 4 in the fourth row rules out all of the gray squares and the third column of the 1st 3x3 square. Additional groups, like the inner 3x3 squares, provide additional constraints that make this strategy more effective with fewer givens; only two 4s outside the completely empty 1st 3x3 square were required to determine where in the 1st 3x3 square the 4 must be placed.
Another strategy that is useful in some puzzles is to determine what values cannot possibly be placed in a particular spot, and if there is only one possible value left, then the spot must hold that value. The values that cannot appear in a spot can be determined by finding all the values that already appear in any of the groups that include the spot. Thus, in example 5 below a 9 must be placed at (1, 1) because it is the only value left that is not already in the 1st 3x3 square, the 1st column or the 1st row.
A 1, 2, or 3 placed at (1, 1) would conflict with the values in row 1. Similarly, a 6, 7, or 8 would conflict with the values in column 1 and both a 4 and 5 can already be found in the 1st 3x3 square. This strategy is often called counting in Sudoku puzzle solving guides.
One deterministic strategy that is often found in advanced Sudoku puzzle solving guides under a wide variety of names is illustrated in the puzzle below. Since only 8 and 9 are missing from the second 3x3 square, they must both be located in the third row, even though which number goes where in the two empty spots cannot yet be determined. This, however, implies that there must be an 8 in the third row in the 2nd 3x3 square, and that 8, therefore, cannot appear in the third row of either the 1st or 3rd 3x3 squares. Additional constraints shown in the puzzle imply that 8 cannot be placed anywhere in the 1st 3x3 square other than at (1, 1).
Unlike the previous techniques that apply equally to rows and columns, this one can only be used when there are two groups that overlap in at least two spots. Thus it can only be applied to 3x3 squares and rows or 3x3 squares and columns in a traditional Sudoku puzzle, because any two rows and columns overlap only in one spot. In the published puzzles that have been evaluated to date, this deterministic strategy has not proven necessary to solve puzzles when the first two deterministic methods are combined. Any moves determined by this strategy can almost always be determined by using only the first two methods, although each empty spot cannot necessarily be determined at the same point in the solution. For this reason, this third strategy is not currently used in the puzzle difficulty key algorithm used to rate puzzles. If a puzzle were designed so that this strategy was required when the first two were insufficient to make progress toward the solution, the current puzzle difficulty algorithm would search for a nondeterministic guess that would allow for a solution. Thus, in effect, the puzzle rating system would rate this or any other type of deterministic strategy that was not implemented in the rating algorithm as a nondeterministic step.
The strategies listed so far are all deterministic because they allow the value to be logically determined without any question or doubt so long as no mistakes have been made in the puzzle. Another technique is called nondeterministic or more colloquially, "guess and check," because it requires guessing that a step is correct without any logical guarantees that it is correct. Nondeterministic steps may not lead to a solution and may in fact lead to a contradiction in the sense that you may reach a point where no value is valid for a spot. If all of your other steps before and after your guess were deterministic and based solely on logic, then by reaching a contradiction you have logically shown that your guess was incorrect and that the value cannot be placed in the spot specified by your guess. Multiple guesses are much more complex and require negative results on all possible combinations to draw any conclusions about the validity of the initial guess. Nondeterministic algorithms that check all possible guesses are often used by computers to solve these puzzles. This technique, however, often proves difficult and error prone for most human solvers. Nevertheless, some puzzles are published that require a nondeterministic step (or guess) and if you reach a point in the solution of a puzzle where it seems that you cannot make any further deterministic progress, you may need to make a guess at that spot and backtrack to the exact same puzzle where you made your guess if you eventually reach a contradiction. Multiple levels of guesses have never proven necessary to solve and rate any published puzzles tested to date. Indeed, many argue that it is not a valid Sudoku puzzle unless there exists a deterministic solution that does not require guessing.
Although there are many other types of deterministic and nondeterministic strategies that can be used to solve these types of puzzles, the two deterministic strategies described above and in the section on computing difficulty keys have been found to be sufficient to solve the vast majority of the published puzzles tested so far. By allowing a single guess (nondeterministic step), all published puzzles tested have been solved. This indicates that these two deterministic strategies are general enough to replace all of the rules and patterns that make up most Sudoku strategy guides.
Puzzle difficulty is ranked using the number of deductive steps required to solve the puzzle. The following names have been chosen for the specified range of solution steps:
| Easiest | 1 or 2 steps |
| Easy | 3 or 4 steps |
| Medium | 5 to 8 steps |
| Difficult | 9 to 14 steps |
| Challenging | 15 to 20 steps |
| Tournament | 21 to 29 steps |
| TournamentPlus | 30 to 45 steps |
| Perplexing | 46 or more steps |
Each deductive step consists of an arbitrary number of logically independent moves that can be determined based only on the puzzle information from the previous step and not on the information from any of the moves of the current step. If you want to know more about deductive puzzle steps and moves, read on.
Puzzles that are too hard, or too easy, can be one of the most frustrating aspects of puzzle solving for both serious and casual solvers. For this reason, rating puzzles is one of the most important parts of creating Sudoku-like puzzles. It is also, however, one of the most difficult. Even apparently simple rating systems, like one to five stars, or "easy," "medium," and "hard," often make assumptions about whether the reader is a serious or casual puzzle solver. The wide variety of Sudoku-like group puzzles types makes ranking puzzles even more complex. The difficulty ranking system used here is designed to help both casual and serious solvers understand the difficulty of a particular puzzle before attempting a solution.
This difficulty ranking system is not just a simple set of group labels. The "Difficulty Key" or DiffKey is a string of digits and the letters A-D that is derived directly from the deductive solution steps, one character for each step in the solution. The meaning of each character for the step is described in detail in the remainder of this section. The "Difficulty" of a puzzle is just the length of this string, and is, therefore, the number of steps in the deductive solution. This single number provides less information than the DiffKey, but more than a simple rating word. Labels like "Medium" or "Challenging" can then also be used to describe ranges of difficulty levels of puzzles for the purposes of grouping puzzles in book sections.
When the character in the DiffKey string for a particular step is a digit from 1 to 8, there are 1 to 8 empty locations that can be deduced directly from just the information given in the puzzle before the step. Thus, a DiffKey of "1" means that the puzzle has only one open empty location, and that location can be filled in based on the information in the puzzle. The digit 9 indicates that nine or more moves are possible in the particular step. Thus, a DiffKey of "9" means that there are nine or more empty locations in the puzzle being rated and that they can all be filled in independently of one another to complete the puzzle. The DiffKey of "993" computed for the indicated puzzle means that there are two different groups of nine or more empty locations and that, once the first group (marked with a 1 in the upper right corner) that can be deduced directly from the puzzle are filled in, the second group of empty locations (marked with a 2) can all be figured out. The 3 at the end of the DiffKey refers to the last three empty cells that cannot be filled in without first filling in some of the ones marked as 2.
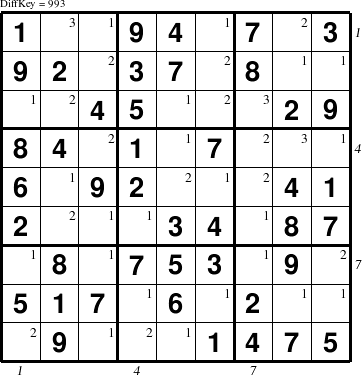
Note, however, that some of the second group can often be deduced once some of the first group are found, but all of the second cannot be completed until all of the first are done. Conversely, a DiffKey that begins "112..." means that there is only one empty location in the given puzzle that can be filled in deductively by this algorithm, and once that single filled in location is deduced, one more empty location can be figured out and filled in, but then two additional moves can be determined using both of those filled in locations, etc.
Moves within a step are deduced by the software using one of two methods. The first method works by eliminating all of the other locations within a group for a particular value, i.e., " The only spot left for a 5 in row N is ..." This method is always tried first for a step and if there are 1 to 8 possible moves using this method, the corresponding digit between 1 to 8 is added to the DiffKey; if there are nine or more moves, a 9 is added to the key for the step.
The second method is only used when no deductions are possible using the first method. This method deduces the value for a location by checking if all other possible values for the location already exist in one or more of the other groups (such as a row or column) that include the location, i.e., " 5 must be place at (X, Y) because it is the only value left that is not in the 1st column, 6th row, or ..." The letter A is added to the DiffKey if there is only one move of this type possible at that step. B is used if there are two possible moves of this type, and so on, with D representing 4 or more possible moves.
A quick glance at a DiffKey gives a lot of information about the solution. Puzzles are simpler to solve when there are fewer steps ( i.e., the DiffKey is shorter). Puzzles are also simpler to solve when there are more moves within each step. For example, a DiffKey that begins "999975" indicates that there are many moves available in each of the first four steps before moves become more restricted in the subsequent two steps. The simplest puzzles have short DiffKey values of all 9s. The most difficult puzzles have long strings of low value digits, from 1 to 3 or so, that indicate deductive bottlenecks. Moves that use deductive method 1, and are represented with digits in the DiffKey, are typically easier for most people to find than deductive moves found using method 2, which are represented using the letters A-D.
There exist many other possible deductive methods to solve Sudoku-like group puzzles beyond the two used to construct DiffKeys. Indeed, the only method that is guaranteed to eventually solve all possible puzzles that can be solved ( i.e., they have a single unique solution), is the non-deterministic guess-and-check method with backtracking. Puzzles without deterministic deductive solutions, however, are typically much harder to solve (at least for humans) and can take much more time (for computers and humans alike) because each guess requires backtracking to the point of the guess if a logical inconsistency is ever encountered after the guess. An asterisk, "*" is added to the DiffKey if neither of the deterministic methods yields a solution and a guess is required to solve the puzzle. The DiffKey algorithm currently rates the puzzle as having no solution DiffKey if a solution cannot be found that requires only a single guess. For this reason, a DiffKey will not contain more than one asterisk. The DiffKey puzzle rating system may be extended in the future to include specific types of non-deterministic steps, as well as other types of deductive deterministic reasoning steps, by defining additional character codes for DiffKey strings which indicate that these types of steps are required at that particular point in the solution.