
TPSA is a small class library implementing the algebra of truncated power series (TPSA) for arbitrary order and number of variables. Addition, subtraction, multiplcation, division, and exponentiation are all implemented in the algebra as overloaded operators. Multiplication is computed with the aid of a hash table, which maps products of pairs of terms to their result terms. The operating system transparently manages the allocation and disposal of memory for intermediate values. There are also a variety of functions, including arithmetic function, that modify the instance and use fewer intermediate values. Those functions are faster. The library is written in VisualBasic.net.
While the class TPSA implements the rudimentary TPSA, the class TPSAMaps is a second class that performs computation with maps, a map being an array of TPSA objects representing a polynomial mapping of a space into itself. The array has as many elements as there are variables of the algebra. In addition to themselves being a TPSA, they may act on each other via function composition. In contrast to multiplications in TPSA, which use a hash table, compositions are computed via a straightforward algorithm. The composition inverse of maps that preserve the origin may be computed. TPSAMaps is not a child class of TPSA, although it relies heavily on TPSA. Initializing TPSAMaps also initializes TPSA, and TPSA is as easily used in concert with TPSAMaps. Below there is a section on usage. See the help file TPSA.chm for a detailed description of the API.
One first initializes the class,
TPSA.init(v, o) TPSAMaps.init(v, o) ' also initializes TPSA
where v and o are integers representating the number of variables and order of TPSA and TPSAMaps. This initializes a number of shared members of the class, a few of which are queried using the syntax:
TPSA.v and TPSAMaps.v
is the number of variables in the TPSA,
TPSA.o and TPSAMaps.o
is the order of the TPSA, and
TPSA.n and TPSAMaps.n
is the number of polynomial terms of the TPSA, i.e., (v+o)!/v!o!.
As shared members, these parameters are accessed through the initialized classes themselves, as opposed to through instances of the classes.
String representations of instances of both TPSA and TPSAMaps are returned by the method ToString.
Other parameters carry further information about the TPSA.
TPSA.order
is an array containing the order (degree) of the corresponding terms;
TPSA.exponents
is a two-dimensional array containing the exponents of the variables of the corresponding terms of the array;
TPSA.hash
is a three-dimensional jagged array representing, for each term, a list of pairs of terms whose product is the term; and
TPSA.vars
an array of TPSA objects corresponding the the variables of the TPSA.
A TPSA variable is declared simply in Visual Basic.Net
dim var as TPSA
while TPSA instances are created through the syntax
var = new TPSA var = new TPSA(Create.Instantiate) var = new TPSA(Create.PointersOnly)
The first and second create zero TPSA objects. The single instance property of instances of TPSA, which carries the Taylor series coefficients, is tps.
dim var as TPSA = new TPSA(Create.Instantiate) var.tps,
which is an array of doubles of length n. The third syntax for instantiating TPSA types creates the pointer object, but not the actual Taylor coefficients. This is useful if one needs to manipulate the underlying tps member, which initially points to Nothing:
dim fctn as TPSA = new TPSA(Create.PointersOnly)
fctn.tps = new double () {1, 2, 3, 4}
Declarations and assignments may be combined in Visual Basic and other languages.
dim v as TPSA = (x + 2 * y)^3
Shared members unique to TPSAMaps are:
TPSAMaps.Id,
the identity map, and
TPSA.zero,
the TPSA zero element.
The single instance property of TPSAMaps is map:
dim m as TPSAMaps = new TPSAMaps(Create.Instantiate) m.map
which is an array of v TPSA objects. There are several constructors for creating maps.
dim m as TPSAMaps = new TPSAMaps dim m as TPSAMaps = new TPSAMaps(Create.Instantiate) dim m as TPSAMaps = new TPSAMaps(Create.PointersOnly) dim m as TPSAMaps = new TPSAMaps(u, v, ...)
The first three are analogs of the corresponding constructors for TPSA. The arguments of the fourth, u, v, ..., are TPSA objects, the number of which should be the same as the number of variables in the TPSA. An ApplicationException exception is thrown if it does not.
Various TPSA constants are created using the shared method one:
var = TPSA.one(i)
where is is an integer = 0, 1, ..., v; i=0 creates a new instance of the unit element of the algebra, while i = 1, ..., v create TPSA elements corresponding to the v variables of the algebra. It is often expendient to assign friendly names to these quantities.
TPSA.init(3, 7) ' three variables, seventh order dim one as TPSA = TPSA.one(0) dim x as TPSA = TPSA.one(1) dim y as TPSA = TPSA.one(2) dim z as TPSA = TPSA.one(3) dim fctn as TPSA = (1 - x^2 - y^2 - z^2).sqrtMethods that reproduce a TPSA object,
t.copy(s) ' copies s to an existing t t.clone ' returns a new copy of t t.Clear ' clears t t.Clear(2.3) ' clears t but sets tps(0) to a number
where s and t are TPSA variables.
Regarding arithmetic operations, the operators + and - have the usual term-by-term meanings, and similarly += and *=. If a, b, c, and d are TPSA objects,
a = b + c a = b * c a = b / c a = b * (c + d)^3 a += b/c + d a = -a + 2.334 a = 3.7*b
As was suggested earlier, arguments in these arithmetic expressions can also be ordinary numbers. There are serveral arithmetic functions that modify the instance. They are faster when used appropriately.
a.Plus(7.1) : a.Minus(7.1) ' add, subtract a double a.Plus(b, c) ' add another TPSA object(s) or list a.Minus(b) ' subtract another TPSA object a.Minus ' the negative a.Times(2.3) : a.Divide(22.1) ' multiply and divide by a double a.Times(b, c) ' multiply by a TPSA object(s) or list a.Divide(b) ' divide by a TPSA object a.Power(4) : a.Power(-3) ' raise to a power
These methods are functions that return the modified instance
Multiplicative inverses, negative powers, and square roots of TPSA objects with non-zero constant parts may be computed.
a = (1 + x).inverse a = (1 + x)^-3 a = (r^2 - x^2 - y^2).sqrt
A TPSA object can be evaluated at numerical arguments using the method eval.
t.eval(1, 2, 3, 4) ' number of args must equal v
t.eval(new double(){1, 2, 3, 4}) ' number of args must equal v
a = b.eval(new double()() {new double() {1, 2, 3, 4}, new double() {5, 6, 7, 8}})
An exception is thrown if the number of arguments is not equal to v.
Terms may be filtered using the method filter and a list of terms to be dropped.
a = b.filter(new Integer () {3, 8, 5, 11})
This function is useful for removing 'nuisance' aberrations, such as defocus and distortion in optics.
The (instance) method order selectively removes terms of various orders based on an integer argument. A positive argument retains terms of order ≤ that argument, while a negative argument retains terms of order ≥ minus that argument.
t = s.order(3) ' terms <= 3 t = s.order(-4) ' terms >= 4
None of the methods of this class modify the instance, but instead return a new TPSAMaps object.
There are copy and clone methods for maps:
s = t.copy(s) s = t.clone
where s and t are maps. Ordinary arithmetic operations on maps act on a component-by-component basis.
a = b + c a = b * c a = b / c a = b * (c + d)^3 a += b/c + d a = -a + 2.334 a = 3.7*b
Map composition is implemented as a method,
t.comp(s)
and the inverse map, which acts on maps preserving the origin, is called with
t.inverse
Maps may be evaluated at numerical values of the variables for ray tracing, using the method eval:
t.eval(1, 2, ...)
which returns an array of doubles.
Like with TPSA objects, the filter method may be used to zero specific coefficients of terms, but with an array for each component of the map. The terms are specified by arrays of term numbers, one for each element of the map member to be zeroed:
t.filter(fx, fy, ...)
where fx, fy, ... are the arrays of integers. It throws an ApplicationException exception if the number of arrays is not the same as the number of variables.
The instance method order for TPSAMaps objects selectively zeros terms of various orders from each part of the map member property using the TPSA method order.
t = s.order(3) ' terms <= 3 t = s.order(-4) ' terms >= 4
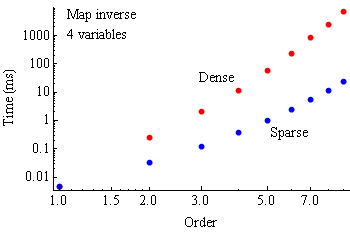
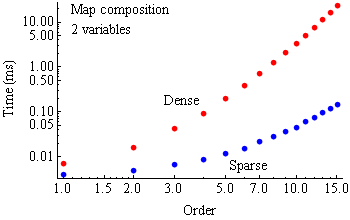
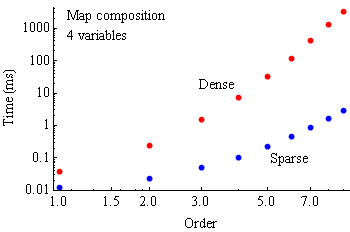
Estimates of computation time on a 2.2-GHz PC on one processor core of the map inverse and map composition functions are given in the graphs below. Performance of the inverse and composition functions vary with the density of the non-zero terms, and traces for the extremes are both plotted.




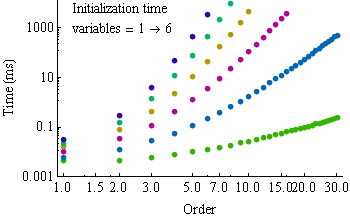
Initialization time as a function of order for the number of variables ranging from one to size is shown on the next plot.
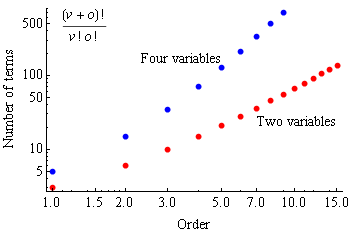
Below is a plot of the number of TPSA terms as a function of order for two and four variables.
The trigonometric functions cos, sin, tan, sec, csc, and cotan; the hyperbolic functions cosh, sinh, tanh, sech, csch, and cotanh; and the Bessel function J0 are coded and have passed a simple test, but have not undergone exhaustive testing.
Several components need to be available.
To use the dynamic link library TPSA.dll instead of the class source file TPSA.vb, attach the dll as a resource to the .NET project. To call functions within the TPSA.dll, prepend the assembly name of the dll, TPSA, to the function name. For example, an earlier example becomes,
TPSA.TPSA.init(3, 7) dim x as TPSA.TPSA = TPSA.TPSA.one(1) dim y as TPSA.TPSA = TPSA.TPSA.one(2) dim z as TPSA.TPSA = TPSA.TPSA.one(3) dim fctn as TPSA.TPSA = 1 - (1 - x^2 - y^2 - z^2).sqrt
This code was developed under Visual Studio 2005 using Visual Basic. It should be possible to build applications combining this code with modules written in other languages, although I haven't tried this.
Nathan Towne
11/2011