There is further help available by typing help <functionname> at the Matlab command line. See the network analyzer module for details about the logic interface, the rfboard API about low-level calls, and network analysis applied to the rf controller for figures and other information.
Fully scripted measurements
Partly scripted measurements using lower-level calls; function details
rfboard API functions for the network analyzer
Graphical interface to the network analyzer in a separate document
At this point there are four scripted measurements: for open-loop response, measuring delays, measuring the loop delay, and measuring proportional-gain behavior.
The naLoopResponse function measures the open-loop response of the controller using a closed-loop measurement. The reference response is the raw response measured at din1_2 with the loop open. One then measures the raw din1_2 response with the loop closed, gains specified. The ratio
r = din1_2closed/din1_2openis related to the open-loop gain G by the relation
r = 1/(1 - G)
The function naLoopResponse also extracts G from the measured r It takes as arguments the interface, a list of value of the proportional gain kp (0 to 1), and a list of the values of the integral gain ki (0 to 1). It also plots the results.
naLoopResponse(0.3, 0.8); % single kp and ki naLoopResponse(0.1:0.1:0.4, 0.8); % traces with varying kp naLoopResponse(0.3, [1 0.3162 0.1 0.03162]);% traces with varying ki
The last line generates the following plot.

The integral/proportional corner is evident in all but the highest integral-gain trace.
The script naDelay.m measures delay between points that have no other frequency response than delay. So, on a bench dout40 → din1_2, din1_2 → cav, etc., can be measured. Just run:
naDelay(12);
The argument is intensity of the excitation as an integer power of two (0 to 15). Then,
Plots on a linear frequency scale of magnitude and phase will appear with the value of the delay printed on the phase plot. The plot below shows the response from din1_2 → cav.

The precision of these delay measurements can be below a nanosecond in quiet environments. Accuracy and precision will no doubt not be this good in a noisy environment measuring a dispersive response function.
As an aside, note from the architecture of fb_loop that there are two routes from e2 to e4, one through the rot_I multiplier, and one through the rot_Q multiplier. Their delays differ by one sample clock. So it of interest to measure the delays through both, by setting the loop-phase to 0 in one case, and to 90º in the other, to verify that the delays are what are expected.
The function naLoopDelay.m directly measures the open-loop delay through the proportional-gain branch using closed-loop measurements.
naLoopDelay(12);
The script sets the proportional gain to some stable value, and changes the loop phase from the nominal to force data through either the e2 → prod1 path, or the e2 → prod2 path, which ever is closer (see fb_loop.v). When the former, fb_loop has a five-clock delay; when the latter, the delay is six clocks. This example is the former.
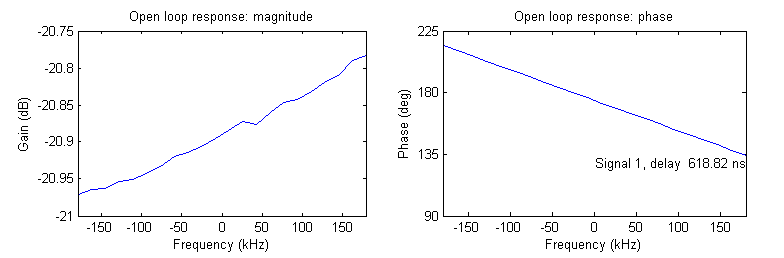
One can verify that the difference between this delay and the din1_t → cav above is the five clocks derived from the logic.
The points e2 and e4 are on either side of the proportional gain block in the module fb_loop, and are also measureable through the debug multiplexor. Feedback is not needed for this measurement, but the output of the controller must somehow find its way to the cavity (cav) input port.
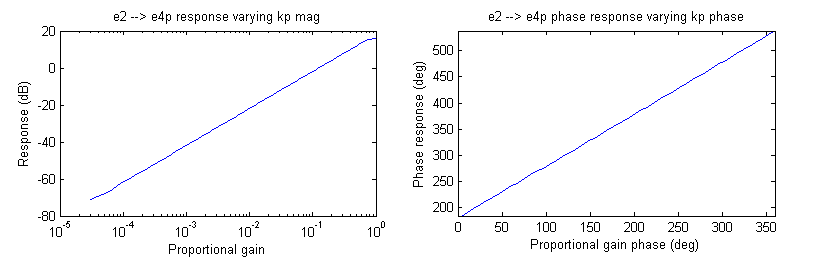
The function naProportionalGainPlot.m performs this measurement, varying the gain and phase on separate plots. All the setup is done by the function. It requires the excitation intensity as an argument (0 to 15).
naProportionalGain(13);
This line generates the following plot.
In contrast to the previous section, in this section Matlab functions manage the network analyzer, data acquisition, and plotting, but not of the setup of the rf controller, such as control of ff enable, debug channel, etc. The function naSequenceSinglePoint runs the network analyzer at a single point. It sets registers, starts the DDS, stops the DDS when done, and reads out the computed Fourier integrals. You can inspect that function to see what is going on.
So this level of scripting requires that conditions of the controller and rf system pertinent to the measurement be set up using a user interface prior to and during running of the scripts. Particularly, feed forward must be enabled. Linear systems do not need a CW rf running, but results from nonlinear systems, such as systems with klystrons, can be operating-point dependent.
global ifc; % handle to the interface data = naSequenceSingleFrequency(ifc, frequency, intensity, timeout);
The returned array data consists of nChans pairs of cosine and sine integrals. Other outputs are available.
One step up is a function that runs the network analyzer at a set of frequencies, returning an array, each element of which is an array containing the frequency followed by naChans of complex-valued responses.
data = naSequence(ifc, frequencies, intensity, timeout);
The parameter intensity must in the 0 to 15 range.
The function naPlot assembles and plots response functions. There are both magnitude and phase plots. It is called at least twice, the first time to register the reference response function, the second and later times to compute and plot the response functions. A scripted measurement looks like this.
% access to the ok interface
global ifc;
disp('User or program setup to measure the reference response function.');
pause;
% first measurement
reference = naSequence(ifc, frequencies, intensity, 10);
% register the reference, giving the indices of the frequency and ref
naPlot(reference(:, [1 3]), 2);
disp('User or program setup to measure the next response function.');
pause;
% next measurement; frequencies must be the same as first
data = naSequence(ifc, frequencies, intensity, 10);
% plot the response giving channel to be plotted
naPlot(data(:, 3), 'log'); % log x plot is default
% can also specify a linear x axis (delay plots)
% naPlot(data(:, 3), 'lin');
% can also specify a function applied to the data prior to plot
% naPlot(data(:, 3), 'lin', @(x)1-1/x);
Further measurements using the same reference can be plotted on the same graphs.
Returns parameters used during network analysis in a structure. Several are hard coded into this function, while others are computed from the frequency and intensity arguments. The structure na is used for setting values used by the instantiated module NetworkAnalyzer.v.
na = naParams(frequency, intensity);
frequency is the frequency at which to compute clocks per output period, the phase increment to be provided to logic, the maximum integration time in terms of the number of modulation periods, and the maximum integration time before worst-case overflow. Damping time and integration time are provided to logic in units of modulation period (1/modulation frequency).
The structure na has fields:
The hard-coded among these parameters must be manually kept in sync with the logic, i.e., when the logic changes, naParams.m must be edited. A better solution would be to code these parameters in the build code.
r = naSequence(ifc, frequencies, maxtime, intensity);
The results array r has as many rows as frequencies, each row consisting of the frequency and the nchans normalized complex-valued response functions of that frequency.
[result f turns time terms] = naSequenceSinglePoint(ifc, frequency, intensity, maxtime);
Arguments:
Returned values:
The raw integrals in result have been divided by the number of terms, but no other normalization has been applied.
Plots the result of a network-anayzer measurement, one figure per channel plotted. It is called twice, the first time to define a reference response against which other response functions are compared. The argument of that call is an array whose first column contains the frequency points, and the second column containing the reference response. When called the second and later times with or without a new measurement, the columns contain the traces to be plotted. They must have been measured at the same frequencies, and have the same number of columns on all those subsequent calls.
% define the reference res = naSequence( ... ); % register the reference naPlot(res(:, [1 refnum]), anynumber); % optional new measurement with different conditions pause; % modify conditions res = naSequence( ... ); % plot the traces naPlot(res(:, channums)[, 'log'|'lin'][, postprocessfunction]);
The refnum and channums arguments are lists of 2-based indices selecting the channels to be reference and plotted, respectively, from among ddsI, debug_dat, s0a, s0b, s1a, s1b, s2a, s2b, s3a, s3b, cav, fwd, rev, din1_2, and inhOut (see the llrf_xem.v source for an up-to-date list) limited by nchans.
The anynumber argument is a numerical flag telling naPlot that this is a reference call.
The optional 'log'|'lin' argument selects logarithmic or linear horizontal scale, respectively (default 'log'). The vertical scale is always linear, expressed in decibels and degrees.
The optional argument postprocessfunction is a function that is applied to the data prior to plotting, needed, for example, when measuring open-loop response using closed-loop measurements. The default is the identity function.
A single response measurement is sufficient when the reference is among the channels measured. But this need not be the case. For example, the measurement of e2 → e4 response cannot be done in one measurement because e2 and e4 are available only through the debug channel. In this case, e2 is first measured with the debug channel set to e2, with a subsequent call of naPlot specifying the debug channel as the reference. Then the debug channel selects e4, another response measurement performed, and naPlot is called again specifying a linear or log plot.
At the moment, the naPlot only plots the debug channel, although the reference channel can be any channel. So only one response function is plotted per naSequence/naPlot run. Modification of these functions is required to plot more that one response function.
At the lowest level, the rfboard API class has methods for accessing network-analyzer logic.
global ifc; % access to the interface update = 1; % update to/from logic noupdate = 0; % no update % set the naFreq frequency parameter, 2.5 kHz ifc.naFreq(144, noupdate); % set the naDamp damping-time parameter of NetworkAnalyzer.v ifc.naDamp(3, noupdate); % set the naAcquire integration-time parameter of NetworkAnalyzer.v ifc.naAcq(77, noupdate); % set the intensity parameter of NetworkAnalyzer.v ifc.naIntensity(13, update); % start the measurement ifc.naStart(); % wait for the integration to finish while ifc.naBusy(update); pause(0.03); end % stop everything ifc.naStop(); % read the data from the network analyzer data = naReadout(16);
naReadout blocks until the integration finishes and it reads out the data. It will not return if no integration was started, or will appear not to return if the integration time is accidentally very long.
The return value data contains 32 double words. The first 2*naChans are pairs of cosine and sine integrals, one pair for each channel. The thirty double-word block is followed by an unused double word, followed by a double-word integration time in clocks. Data length is fixed at 128 bytes.
The sine and cosine integrals are normally assembled into complex numbers that represent the complex-valued responses. Those responses alone have no normalization. They acquire quantitative meaning only after they are divided by a reference response separately measured in the measurement procedure. This reference response can be as simple as the reference channel 0 measuring the ddsI signal, or can be something more involved such as the open-loop din1_2 response mentioned in the open-loop response section. The needed reference depends on what is being measured. In any case it is these sorts of considerations that are embedded in the scripted measurements of the first major section above, and are common to analog network response measurements.